Mechanika budowli
Wzory transformacyjne metody przemieszczeń
- Wzory transformacyjne w metodzie przemieszczeń
- Pręt obustronnie utwierdzony
- Pręt utwierdzony-przegubowy
- Wersja PDF
Wzory transformacyjne w metodzie przemieszczeń
Równania transformacyjne, znane również jako równania nachylenia-ugięcia (ang. slope-deflection equations), stanowią fundament metody przemieszczeń. Pozwalają one w sposób jawny wyrazić siły na końcach pręta (momenty i siły tnące) jako funkcję nieznanych przemieszczeń węzłowych: kątów obrotu (\(\varphi\)) oraz przemieszczeń liniowych, które powodują obrót cięciwy pręta (\(\psi\)). Poniżej przedstawiono wzory dla dwóch podstawowych przypadków podparcia pręta w układzie podstawowym.
Pręt obustronnie utwierdzony

Wzajemne przemieszczenie końców pręta i wynikający z niego kąt obrotu cięciwy opisują następujące wzory:
\[ \Delta = y_k - y_i \] \[ \psi_{ik} = \frac{\Delta}{L} = \frac{y_k - y_i}{L} \]Dla pręta \(ik\) utwierdzonego obustronnie o stałej sztywności, ogólna postać tych równań to:
\[ M_{ik} = 2EK_{ik}(2\varphi_i + \varphi_k - 3\psi_{ik}) + M_{ik}^P \] \[ M_{ki} = 2EK_{ik}(2\varphi_k + \varphi_i - 3\psi_{ik}) + M_{ki}^P \]Wzory na siły tnące na końcach pręta \(ik\) mają postać:
\[ Q_{ik} = -6E\frac{I_{ik}}{L_{ik}^2}(\varphi_i + \varphi_k - 2\psi_{ik}) + Q_{ik}^P \] \[ Q_{ki} = -6E\frac{I_{ik}}{L_{ik}^2}(\varphi_k + \varphi_i - 2\psi_{ik}) + Q_{ki}^P \]Gdzie poszczególne symbole oznaczają:
- \(M_{ik}, M_{ki}\) – szukane momenty na końcach \(i\) oraz \(k\) pręta.
- \(E\) – moduł Younga.
- \(K_{ik} = I_{ik}/L_{ik}\) – sztywność pręta.
- \(\varphi_i, \varphi_k\) – niewiadome kąty obrotu na końcach pręta.
- \(\psi_{ik} = \delta/L_{ik}\) – kąt obrotu cięciwy pręta, wynikający z wzajemnego przemieszczenia liniowego końców.
- \(M_{ik}^P, M_{ki}^P\) – tzw. momenty od utwierdzenia, powstałe od obciążeń zewnętrznych.
- \(Q_{ik}^P, Q_{ki}^P\) – siły tnące w belce od obciążeń zewnętrznych.
Pręt utwierdzony-przegubowy
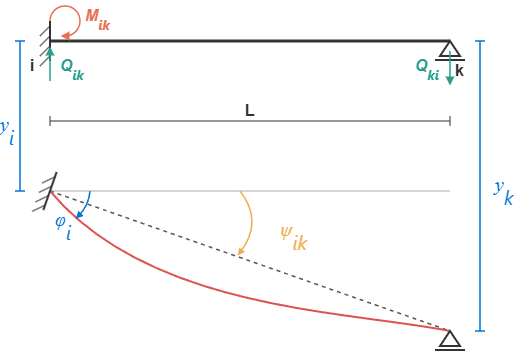
Gdy jeden z końców pręta (np. koniec \(k\)) jest w rzeczywistości podparty przegubowo, wiemy, że ostateczny moment w tym miejscu musi być równy zeru (\(M_{ki} = 0\)). Ta wiedza pozwala na uproszczenie ogólnych równań transformacyjnych. Eliminując z układu równań kąt obrotu przegubu \(\varphi_k\), otrzymujemy jedno, uproszczone równanie na moment w utwierdzeniu (\(i\)):
\[ M_{ik} = 3EK_{ik}(\varphi_i - \psi_{ik}) + M_{ik}^P \]Wzory na siły tnące na końcach pręta \(ik\) mają postać:
Dla pręta z przegubem na końcu \(k\), wzory upraszczają się do postaci:
\[ Q_{ik} = -3E\frac{I_{ik}}{L_{ik}^2}(\varphi_i - \psi_{ik}) + Q_{ik}^P \] \[ Q_{ki} = -3E\frac{I_{ik}}{L_{ik}^2}(\varphi_i - \psi_{ik}) + Q_{ki}^P \]