Método de Wereszczagin

Introducción al método de Wereszczagin

Si te interesa la derivación del método de Wereszczagin - echa un vistazo a nuestro diccionario de términos.

Fundamentos del método de Wereszczagin

Wereszczagin observó que:

\[u=\int \frac{M_g \cdot M_1}{E I} \cdot dx=\frac{1}{E I} \cdot \Omega \cdot \eta\]

Si tenemos que integrar figuras (es decir, en la práctica funciones), de las cuales:

• una es o puede ser parabólica (función cuadrática, bajo carga continua constante) - será el gráfico en el estado inicial (a partir de las cargas dadas),
• la otra es no parabólica - será el estado unitario, al calcular los desplazamientos será el gráfico de la fuerza unitaria aplicada en el lugar y en la dirección del desplazamiento buscado - Ver más sobre este tema - Método de Maxwell-Mohr,

el resultado de tal integración podemos reducir a la fórmula:

\[u=\Omega \cdot \eta\]

donde:

• \( \Omega \) - área de la figura en el gráfico de momentos en el estado P,
• \( \eta \) - ordenada en el gráfico en el estado unitario en el lugar (a la altura) del centro de gravedad de la figura del estado P.

La imagen siguiente lo representa gráficamente.

Algunas observaciones prácticas

1) ¿Qué significa realmente si el desplazamiento resulta negativo?

Esto significa que la dirección del desplazamiento será opuesta a la dirección de la fuerza unitaria que hemos asumido.

En el caso de un desplazamiento vertical en el punto B, se asumió una fuerza unitaria con dirección hacia abajo, el desplazamiento resultó negativo, lo que significa que en realidad será hacia arriba. La dirección de la fuerza unitaria correspondiente al ángulo de rotación buscado en el punto A se asumió como un momento en sentido horario.

2) Signos al integrar

Al integrar con el método de Wereszczagin, debemos prestar atención a si las áreas de las figuras integradas están del mismo lado de la barra o del lado opuesto. Si están del mismo lado, el resultado de esta integración única es positivo, si están en lados opuestos - es negativo.

3) Descomposición en figuras simples

Otra cosa importante es la descomposición en figuras simples. Tanto el gráfico del estado P como el del estado unitario, si es una figura más complicada que: un rectángulo, un triángulo rectángulo, una parábola, podemos y debemos descomponer mentalmente en figuras simples.

Ejemplos de descomposición en figuras simples

Trapecio 1

Ejemplo similar al que consideramos al derivar el método de Wereszczagin.

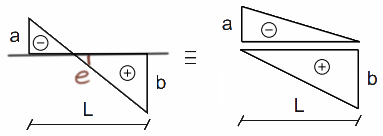
Trapecio 2

Ahora una figura que realmente identificamos a primera vista como un trapecio.

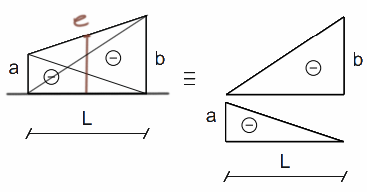
A veces es útil calcular el valor en la mitad del gráfico, ¿cómo se puede hacer fácilmente?

Si el gráfico cambia linealmente, entonces en la mitad es la media aritmética de los dos números extremos, por ejemplo:

• en la figura 1. \( e=\frac{-a+b}{2} \),
• en la figura 2. \(e=\frac{-a-b}{2} \),

Si el gráfico cambia de manera parabólica, entonces a esta media se le debe sumar o restar el valor \( f=\frac{q\cdot l^2}{8} \) que representa la protuberancia de la parábola, que se produce si tenemos una carga continua en el elemento.

Así que \( e=\frac{a+b}{2}\pm \frac{q\cdot l^2}{8} \), donde si sumamos más o menos depende de si la acción de la carga continua hace que la parábola sea convexa o cóncava, de hecho, miren los ejemplos a continuación.

Triángulo-parábola

La acción de la carga continua hace que la parábola sea convexa, así que \( e=\frac{0+a}{2}+\frac{q\cdot l^2}{8} \)

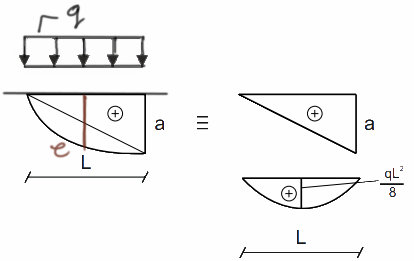
Trapecio parabólico 1

Ahora algo más interesante y en realidad no puede haber nada más difícil que los dos siguientes casos.

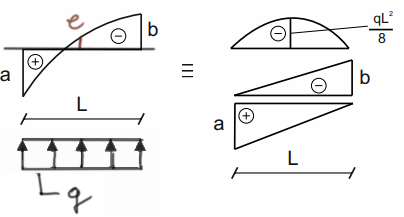
\( e=\frac{a+(-b)}{2}-\frac{q\cdot l^2}{8} \)

Trapecio parabólico 2

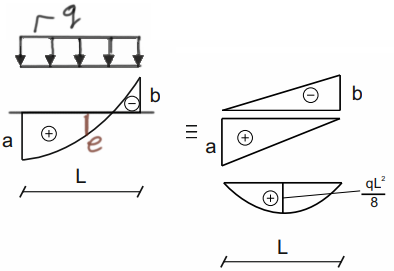
\( e=\frac{a+(-b)}{2}+\frac{q\cdot l^2}{8} \)

Trapecio parabólico 3

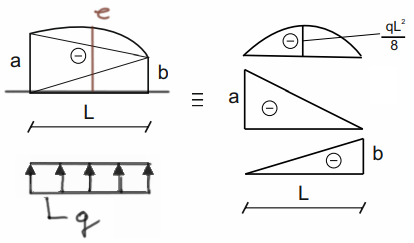
\( e=\frac{-a+(-b)}{2}-\frac{q\cdot l^2}{8} \)

Trapecio parabólico 4

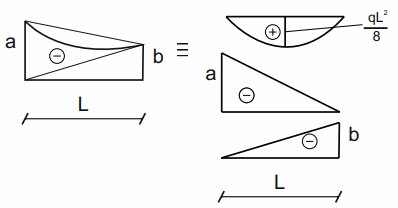
\( e=\frac{-a+(-b)}{2}+\frac{q\cdot l^2}{8} \)

Trapecio parabólico 5

Creo que el principio de funcionamiento ya está claro.

Por último, otro caso problemático al principio. Debemos recordar que si la carga continua no es perpendicular a la barra, al descomponer en figuras simples, al calcular la altura de la parábola \( f \) como longitud tomamos la longitud de acción de la carga continua, y no la longitud de la barra!. Ver el ejemplo a continuación

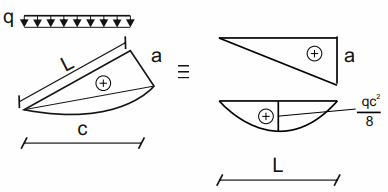
\( e=\frac{0+a}{2}+\frac{q\cdot c^2}{8} \)

Fórmulas/tablas de Wereszczagin

A menudo se utilizan también las fórmulas derivadas utilizando el método de Wereszczagin. En principio, todos los posibles integrales podemos calcular utilizando cuatro fórmulas:

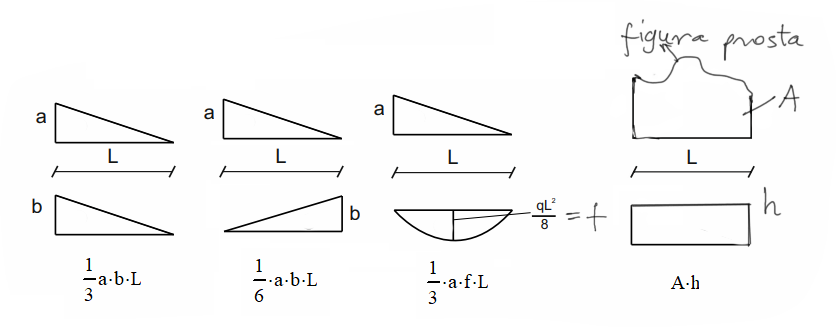
En cada integración prestamos atención a los signos de las figuras integradas, si son iguales tenemos un resultado positivo, si son opuestos, negativo.

Fórmulas:

1. Triángulo con triángulo -> si las alturas están del mismo lado, según la fórmula sería \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{2}{3} \cdot b \) lo que nos da, tras simplificar, la fórmula final \( \frac{1}{3} \cdot a \cdot b \cdot L \)
2. Triángulo con triángulo, alturas en lados opuestos -> \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{1}{3} \cdot b=\frac{1}{6} \cdot a \cdot b \cdot L \)
3. Triángulo (cualquier orientación) con parábola -> ¡Atención! Al integrar con la parábola, el área debe calcularse desde la parábola, y la ordenada desde la otra figura. \( \Omega \cdot \eta = \frac{2}{3}\cdot f \cdot L\cdot \frac{1}{2} \cdot a=\frac{1}{3} \cdot a \cdot f \cdot L \)
4. Cualquier figura con un rectángulo -> por definición será el área de esa figura multiplicada por la ordenada del rectángulo, que tiene la misma altura "h" en todas partes. \( \Omega \cdot \eta = A \cdot h \)

Donde cualquier figura, tras la descomposición en figuras simples, será:

• triángulo
• rectángulo
• o parábola

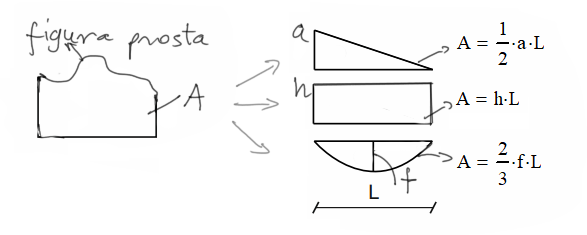
Algunos utilizan una mayor cantidad de fórmulas, se pueden multiplicar realmente muchas, sin embargo, estas cuatro más la descomposición en figuras simples son suficientes para manejar cualquier situación. Por supuesto, calcular desde la definición y no recordar fórmulas ya preparadas también siempre estará bien.

Por ejemplo, a continuación una tabla del libro del Dr. Marian Paluch
(AGH, Fundamentos de la Mecánica de Estructuras, Cracovia 2003)

De la fórmula tercera desde arriba y tercera desde abajo, los estudiantes de AGH la utilizan especialmente a menudo :)