Wereszczagin method

Introduction to the Wereszczagin method

If you are interested in deriving the Wereszczagin method - check our glossary of terms.

Basics of the Wereszczagin method

Wereszczagin noticed that:

\[u=\int \frac{M_g \cdot M_1}{E I} \cdot dx=\frac{1}{E I} \cdot \Omega \cdot \eta\]

If we have to integrate figures (which in practice means functions), from which:

• one is or can be parabolic (quadratic function, under constant uniform load) - this will be the graph in the Initial state (from the given loads),
• the other is non-parabolic - this will be the unit state, when calculating displacements this will be the graph from the unit force applied at the location and in the direction of the sought displacement - See more on this topic - Maxwell-Mohr method,

the result of such integration can be reduced to the formula:

\[u=\Omega \cdot \eta\]

where:

• \( \Omega \) - area of the figure on the moment diagram in state P,
• \( \eta \) - ordinate on the unit state diagram at the location (at the height) of the center of gravity of the figure from state P.

The image below illustrates this graphically.

Some practical notes

1) What does it actually mean if the displacement comes out negative?

It means that the direction of the displacement will be opposite to the direction of the unit force we assumed.

In the case of vertical displacement at point B, a unit force was assumed with a downward direction, the displacement came out negative, which means that in reality it will be upward. The direction of the unit force corresponding to the sought angle of rotation at point A was assumed to be a right-handed moment.

2) Signs during integration

When integrating using the Wereszczagin method, we must pay attention to whether the areas of the integrated figures are on the same side of the beam or on opposite sides. If they are on the same side, the result of that single integration is positive; if on opposite sides - it is negative.

3) Decomposition into simple figures

Another important thing is decomposition into simple figures. Both the graph from state P and from the unit state, if it is a more complicated figure than: rectangle, right triangle, parabola, we can and will mentally decompose into simple figures.

Examples of decomposition into simple figures

Trapezoid 1

An example similar to the one we considered when deriving the Wereszczagin method.

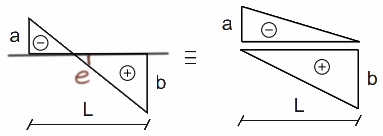
Trapezoid 2

Now a figure that we actually identify at first glance as a trapezoid.

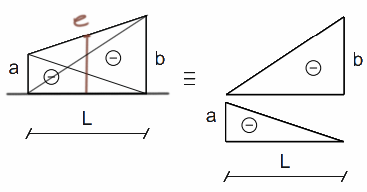
Sometimes it is useful to calculate the value in the middle of the graph, how can this be easily done?

If the graph changes linearly, then in the middle is the arithmetic mean of the two extreme numbers, for example:

• in fig.1 \( e=\frac{-a+b}{2} \),
• in fig.2 \(e=\frac{-a-b}{2} \),

If the graph changes parabolically, then to this average we need to add or subtract the value \( f=\frac{q\cdot l^2}{8} \) representing the bulge of the parabola, which occurs if we have a continuous load on the element.

So \( e=\frac{a+b}{2}\pm \frac{q\cdot l^2}{8} \), where whether we add plus or minus depends on whether the action of the continuous load causes the parabola to be convex or concave, by the way, see the examples below.

Triangle-parabola

The action of the continuous load causes the parabola to be convex, so \( e=\frac{0+a}{2}+\frac{q\cdot l^2}{8} \)

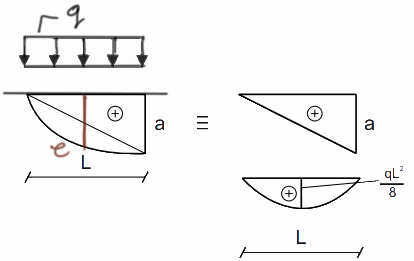
Parabolic trapezoid 1

Now something more interesting and basically nothing more difficult than the next two cases can happen.

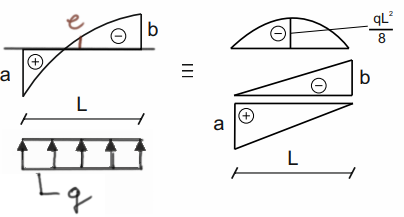
\( e=\frac{a+(-b)}{2}-\frac{q\cdot l^2}{8} \)

Parabolic trapezoid 2

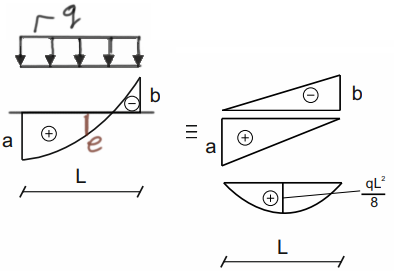
\( e=\frac{a+(-b)}{2}+\frac{q\cdot l^2}{8} \)

Parabolic trapezoid 3

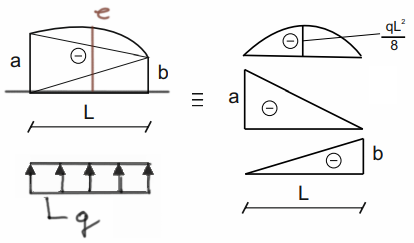
\( e=\frac{-a+(-b)}{2}-\frac{q\cdot l^2}{8} \)

Parabolic trapezoid 4

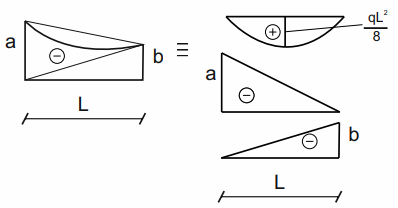
\( e=\frac{-a+(-b)}{2}+\frac{q\cdot l^2}{8} \)

Parabolic trapezoid 5

I think the principle of operation is already clear.

Finally, one more troublesome case at the beginning. We must remember that if the continuous load is not perpendicular to the beam, then when decomposing into simple figures, when calculating the height of the parabola \( f \) as the length we take the length of the action of the continuous load, and not the length of the beam!. See the example below

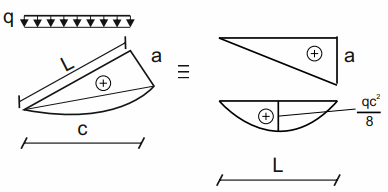
\( e=\frac{0+a}{2}+\frac{q\cdot c^2}{8} \)

Wereszczagin formulas/table

Derived formulas using the Wereszczagin method are also frequently used. In principle, all possible integrations can be calculated using four formulas:

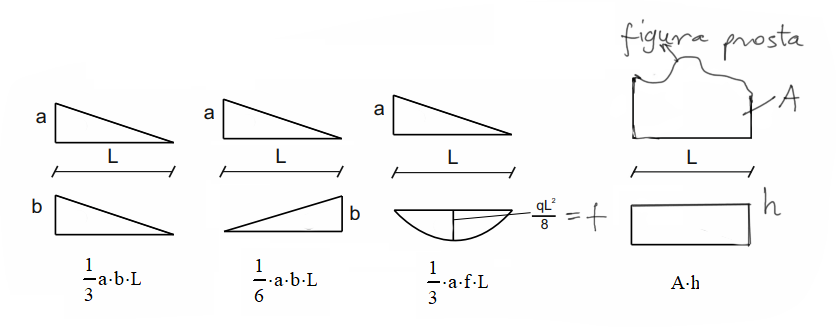
When integrating, we pay attention to the signs of the integrated figures; if they are the same, we have a positive result; if opposite, it is negative.

Formulas:

1. Triangle with triangle -> if the heights are on the same side, then according to the formula it would be \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{2}{3} \cdot b \) which gives us the final formula \( \frac{1}{3} \cdot a \cdot b \cdot L \)
2. Triangle with triangle, heights on opposite sides -> \( \Omega \cdot \eta = \frac{1}{2}\cdot a \cdot L\cdot \frac{1}{3} \cdot b=\frac{1}{6} \cdot a \cdot b \cdot L \)
3. Triangle (arbitrarily rotated) with parabola -> Note! When integrating with a parabola, the area must be calculated from the parabola, and the ordinate from the other figure. \( \Omega \cdot \eta = \frac{2}{3}\cdot f \cdot L\cdot \frac{1}{2} \cdot a=\frac{1}{3} \cdot a \cdot f \cdot L \)
4. Any figure with a rectangle -> by definition, this will be the area of that arbitrary figure times the ordinate from the rectangle, which has the same height "h" everywhere. \( \Omega \cdot \eta = A \cdot h \)

Where any figure, after decomposition into simple figures, will be:

• triangle
• rectangle
• or parabola

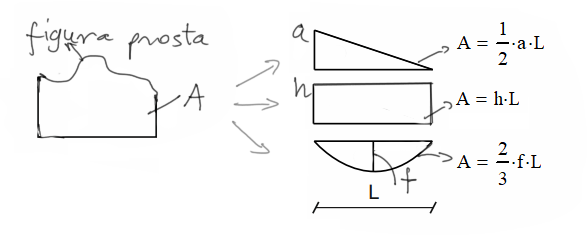
Some use a larger number of formulas; they can really be multiplied many times, but these four plus decomposition into simple figures will be enough to handle any situation. Of course, calculating from definitions and not remembering ready-made formulas will also always be fine.

For example, below is a table from Dr. Marian Paluch's book
(AGH, Basics of Structural Mechanics, Kraków 2003)

Students at AGH particularly often use the third formula from the top and the third from the bottom :)